还是继续数值计算方法的讨论。本文想简要介绍一下如何用迭代法计算方程和方程组的根。这一次的难度低了很多,我写着也是轻松了不少。
迭代法求解方程最核心的是利用不动点进行不动点迭代。
不动点迭代
在高中阶段你可能学习过这样的叫蛛网图的东西:
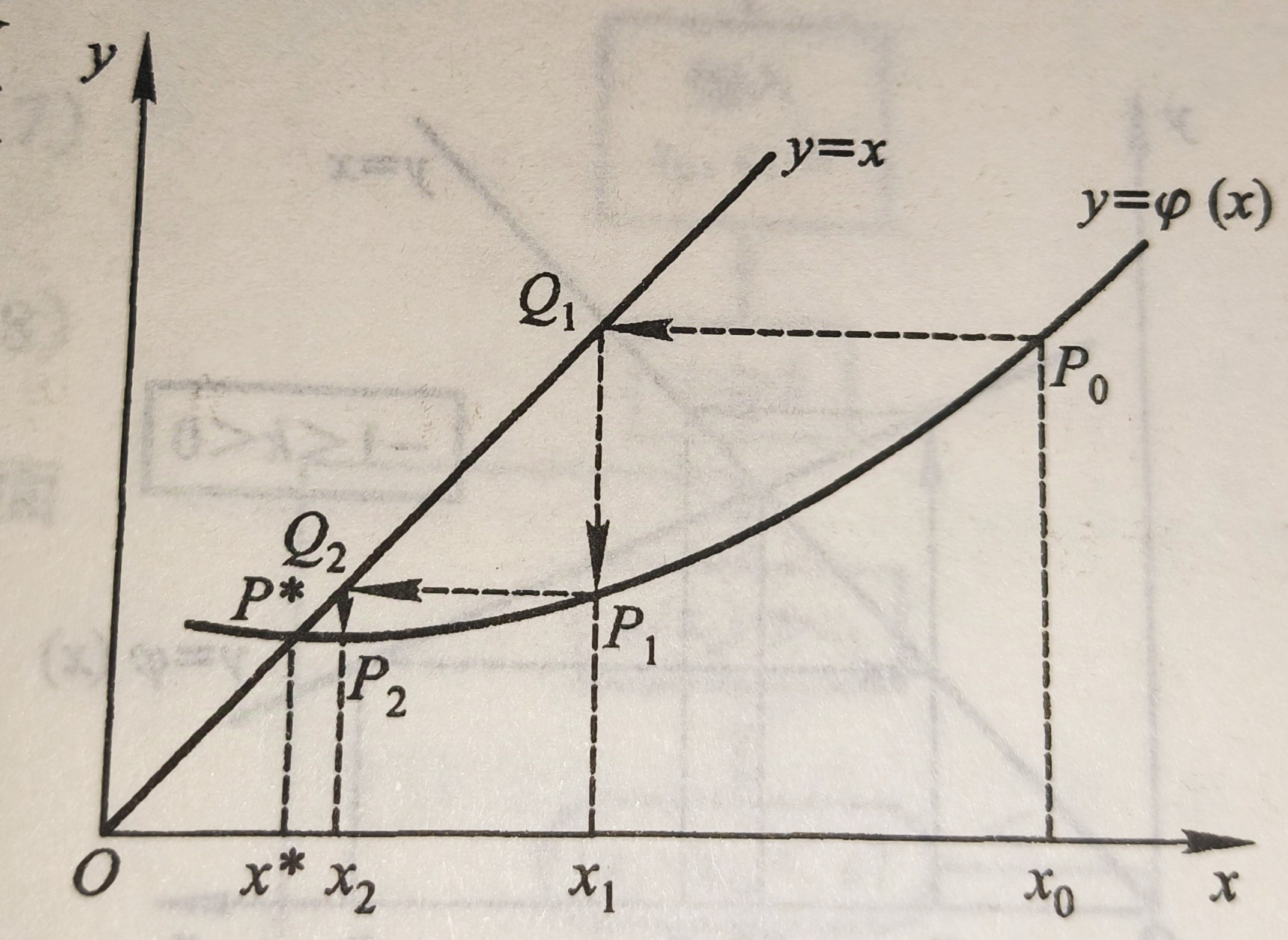
蛛网图迭代的极限就是函数的不动点。
所谓不动点迭代就是利用了这样的性质。
一般地,我们想求解方程f(x)=0,如果我们可以将这个方程转化为x=g(x),那么g(X)的不动点就是f(x)的零点。
而g(x)的不动点又是蛛网图迭代的极限。
如果用代数语言表示的话,就是迭代公式
$$x_{k+1}=g(x_k)$$这就是不动点迭代求方程的根的方法。
当然,如果要更严谨化的说明的话,就是下面的压缩映像原理:
设g(x)在[a,b]上具有连续的一阶导数,且满足以下条件:
1.$\forall x \in [a,b],g(x) \in [a,b]$
2.$\exist 0 \le L <1,s.t. \forall x\in [a,b],|g’(x)|\le L$
则迭代过程
$x_{k+1}=g(x_k)$收敛,且有误差估计式:
$|x^*-x_k|\le \frac{L^k}{1-L}|x_1-x_0|$
这个是简化版的压缩映像原理了,如果你学过《泛函分析和实变函数》那么你见到的压缩映像原理应该是这样的:
设(X,d)是完备的距离空间,T是其中自身到自身的映射即X→X,如果$\forall x,y\in X,\exist L\in(0,1), d(Tx,Ty) \le Ld(x,y)$(满足这样条件的映射称为压缩映射),则存在唯一的$x^$使得$Tx^=x^*$
用一句话来说就是,完备的距离空间上到自身的压缩映射必有唯一不动点。
别扯那么多了,还是看简化版的吧。简化版还有误差估计式嘞。
从简化版的误差估计式看,k越大估计值$x_k$会离准确值$x^*$越来越近。
这就足以为不动点迭代法背书了。
但是这里需要注意的是,无论是泛函分析里加强版的压缩映像原理还是我们这里的简化版压缩映像原理,它都是不动点存在的充分条件而不是必要条件。也就是说,如果你找到一个函数他不满足上面的条件,你其实是不能判定他不存在不动点的。在这里我也看到某些教材在这个地方出现了纰漏。
如果严格按照定理的说法只使用定理的话,我们是没有办法判定某个函数不具备不动点的。
除此之外,还有一个更重要的问题也更严重的问题。
无论是简化版的压缩映像原理还是加强版的,我们都要求你找到一个严格大于0,严格小于1的常数L,可是在实践中经常有人把这个条件简化为$g’(x)\le1$这也是不对的。
不动点迭代的收敛速度
收敛性是已经知道了的,毕竟误差估计式都给出来了。但是各个不动点迭代的收敛速度还是有差别的。
我们来考虑第k次迭代后的迭代误差$e_k=x^*-x_k$,如果下一次迭代的迭代误差在k趋于无穷大时和$e_k$的p次方是同阶无穷小我们就说这个迭代是p阶收敛的。
特别的,p=1称为线性收敛,p=2是平方收敛。
那我怎么知道一个迭代方法是几阶收敛的呢?其实很简单,我们要求解的是x=g(x)嘛,你在$x=x_k$处把$x^*$泰勒展开一下。
$g(x_k)=g(x^)+g’(\alpha)(x^-x_k)+\frac{g’’(\alpha)}{2}(x_k-x^*)^2+…$
因为我们求解的是x=g(x),所以$e_k=x^-x_k=g(x^)-g(x_k)=g’(\alpha)(x^-x_k)+\frac{g’’(\alpha)}{2}(x_k-x^)^2+…$
所以如果g(x)在不动点$x^*$附近的1阶导,2阶导,3阶导,…,p-1阶导都是0,而p阶导不为0,不就说明它是p阶收敛的了?
这不就结了。
接下来的迭代方法都是基于不动点迭代得出的,所以他们的收敛速度也是用这个方法求解的,就不多嘴了。
迭代法的加速
现在我们分析出了不动点迭代的收敛速度,那么问题就来了,有些时候这个收敛速度非常慢,有没有办法加快?
可以的,我们还是用误差事后估计的方法加速,这个方法好像每一节都有的样子你应该也熟悉了吧。
针对迭代公式$x_{k+1}=g(x_k)$,它与准确值的误差$x^-x_{k+1}=g(x^)-g(x_k)=g’(\alpha)(x^*-x_k)$
又是拉格朗日中值定理,how old are U?(怎么老是你?)
我们还是认为g(x)的导数值变化不大,是一个常数L,则我们估计出了$x_{k+1}$的误差,从而可以得到更好的近似值也就是把$x^*$解出来,得到
$x^*\approx \frac{1}{1-L}x_{k+1}-\frac{L}{1-L}x_k$
这是一个更好的近似值,接下来再用这个更好地近似值进行迭代这就实现了加速。
埃特金算法
但是上面的加速方法还可以优化一下,其最大的问题就是这个L取啥。
其实这个问题也很简单,我们直接不想了啊哈哈。
直接解决掉问题本身,解决掉提出问题的人。
额我的意思是,我们把L消了。
你再迭代一次得到$x_{k+1}’=g(x_{k+1})$,然后再用拉格朗日中值定理得到
$x^-x_{k+1}’\approx L(x^-x_{k+1})$
和前面第一次迭代得到的$x^-x_{k+1}=L(x^-x_k)$相除就消掉L了,这样就不用考虑了。
然后我们把$x^$解出来,得到$x^=x_{k+1}’-\frac{(x_{k+1}’-x_{k+1})^2}{x_{k+1}’-2x_{k+1}+x_{k}}$
这又是更好的近似值,然后把这个近似值代入原来的迭代公式进行迭代,这也实现了加速。这就是埃特金算法。
牛顿迭代法
我们说了这么多其实都是基于已经将这个方程转化为x=g(x),然后用迭代公式$x_{k+1}=g(x_k)$求解。
但是我们不知道如何把方程转化为x=g(x),牛顿迭代法就是解决了这个问题。
思路其实也非常简单,我们知道微分有dy=f’(x)dx,于是$f(x)-f(x_k) \approx f’(x_k)(x-x_k)$。
从而$f(x)=f(x_k)+f’(x_k)(x-x_k)=0$
那么$x=x_k-\frac{f(x_k)}{f’(x_k)}$,完成啦!
我们把f(x)=0转化为了x=g(x)的形式了,从而再使用不动点迭代得到f(X)根的迭代公式:
$x_{k+1}=x_k-\frac{f(x_k)}{f’(x_k)}$
这就是牛顿迭代法。
用前面的收敛速度的计算方法可以得到在f(x)=0只有单根的情况下,在单根附近牛顿迭代法是平方收敛的。
牛顿下山法
注意,我说的是在f(x)=0只有单根的情况下,在单根附近牛顿迭代法是平方收敛的。
很多时候函数有多根结论就未必是这样的。
更有甚者,你的初值点离根太远,牛顿迭代法可能会发散。
所以就有了牛顿下山法,为我们选择一个合适的初值点。
牛顿下山法是下山法+牛顿法。所谓下山法,就是在不动点迭代的基础上要求每次迭代函数值的绝对值都要下降,也就是要求$|f(x_{n+1})|\le|f(x_k)|$,显然这样的话每次迭代函数值都更接近0,也就有很大的概率是更接近方程的根的。
但是事情往往不是那么美妙,因为咱们暂时还没有科学的方法找到下一个迭代的点。
这时可以把牛顿法引入进来,我们先用牛顿法进行一次迭代得到
$x_{k+1}=x_k-\frac{f(x_k)}{f’(x_k)}$
然后把这个$x_{k+1}$和$x_k$加权平均作为新的$x_{k+1}'$
也就是$x_{k+1}’=\lambda x_{k+1} + (1-\lambda)x_k=x_k-\lambda\frac{f(x_k)}{f’(x_k)}$
这里$0<\lambda \le1$被称为下山因子,我们就是每次迭代找这么一个合适的下山因子。
而下山因子怎么找呢?二分呗。
诶等等二分法?
二分法不也可以求方程的根?
所以很多时候我们也会用二分法先得到一个精确解的范围,然后把初值定在里面,然后再用牛顿法或者牛顿下山法。
弦截法
到这里看起来已经非常完美了,至少我是这么认为的。
但是实际上,有极少部分函数的导数是很难求解的,所以我们要用差商估计导数,这就是弦截法了。
用$f’(x) \approx \frac{f(x_k)-f(x_0)}{x_k-x_0}$代入牛顿迭代法,就是弦截法了。
如果用$f’(x) \approx \frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}$代入牛顿迭代法,就是快速弦截法了。
线性方程组迭代的收敛性
前面说的都是非线性方程,那线性方程呢?一元的情况确实不用费心了,我口算都给你解了。
但是现实里的线性方程组往往阶数非常高,所以也需要一个高效的求解方法。我们还是先介绍迭代法。方法其实和前面是类似的所以一并讲解。
线性方程组AX=b如果我们可以将其化为X=BX+f,那么用前面所说的不动点迭代法就有迭代公式
$X_{k+1}=BX_k+f$
这是我们线性方程组迭代法的基石。
它的误差:
$e_{k+1}=|x^-x_{k+1}|=|BX^+f-(BX_{k}+f)|=B|X^*-X_k|=Be_k$
从而,$e_k=B^ke_0$
那么如果$B^k$能收敛于0的话该迭代法就收敛了,用线性代数或者高等代数的知识就能明白这等价于B的谱半径(最大特征值)小于1。
现在我们有了对于所有矩阵的收敛性判别法,而对于一些特殊的矩阵不用这么麻烦。
比如,对角占优方程组他的雅可比迭代和高斯-赛德尔迭代都是收敛的。
这两种迭代方法我们等下讲,但因为这个话题在这了嘛所以我就先说了。
证明的话因为没说迭代方法,所以也讲不了,其实你也可以等下自己试试看能不能证出来。
我只在这里说一下什么是对角占优方程组。
它指的是系数矩阵是对角占优矩阵的方程组。
OK,说了和没说一样。
所谓对角占优矩阵说的是,主对角线上的元素的绝对值>同行其他元素的绝对值之和的矩阵。
这就明白了吧。
而且这个名字现在看着是不是很直观?主对角线上的元素绝对值比你一整行其他元素绝对值的和都大,那是在这一行绝对的制霸啊。
这样的矩阵其实一定是可逆阵,这个你也可以证明看看。
雅可比迭代
现在的问题还是和前面一样的,不动点迭代法说的轻巧,但是你怎么把AX=b转化成X=BX+f呢?
其中的一种方法就是雅可比迭代法了。
对方程组AX=b,我们将A分解为对角阵D,下三角矩阵L,上三角矩阵U使得
A=D-L-U。
(值得一提的是,这个分解是相当容易的,D就是A的对角元,L取A的下三角去掉主对角线,U取A的上三角去掉主对角线即可)
那么AX=b就是
(D-L-U)X=b
然后移项得
DX=(L+U)X+b
从而$X=D^{-1}(L+U)X+D^{-1}b$
完事了,已经变成X=BX+f的形式了,所以就有迭代公式
$X_{k+1}=D^{-1}(L+U)X_k+D^{-1}b$
这就是雅可比迭代法了。
但是这个方法可以稍微变一下,我们移项的时候不一定要把L和U全部移走,这就是高斯-赛德尔迭代法了。
高斯-赛德尔迭代法
还是安装雅可比迭代的步骤我们得到,(D-L-U)X=b移项但是只移U得到
(D-L)X=UX+b
然后得到$X=(D-L)^{-1}UX+(D-L)^{-1}b$
于是就有迭代公式$X_{k+1}=(D-L)^{-1}UX_k+(D-L)^{-1}b$
但是我们一般不会这么使用,而是再等式两边再乘以D-L得到
$(D-L)X_{k+1}=UX_k+b$
从而$DX_{k+1}=LX_{k+1}+UX_k+b$
所以$X_{k+1}=D^{-1}LX_{k+1}+D^{-1}UX_k+D^{-1}B$
这才是我们一般最爱用的高斯-赛德尔迭代公式。
其实到这里,你应该也能自己造出第三个迭代公式了吧。高斯-赛德尔迭代只移了U,那我只移动L行不行?当然也行啊,反正思路就是这么个思路,怎么折腾随便你。